Fragment Based Methods
Fragment-based methods are a series of reduced-scaling quantum chemistry approximations which rely on the near-sighted nature of electronic matter to circumvent the highly non-linear scaling of traditional electronic structure methods. This page is meant as a non-rigorous introduction to the concept. Other sections in this documentation present the methods in a more rigorous manner.
The Problem
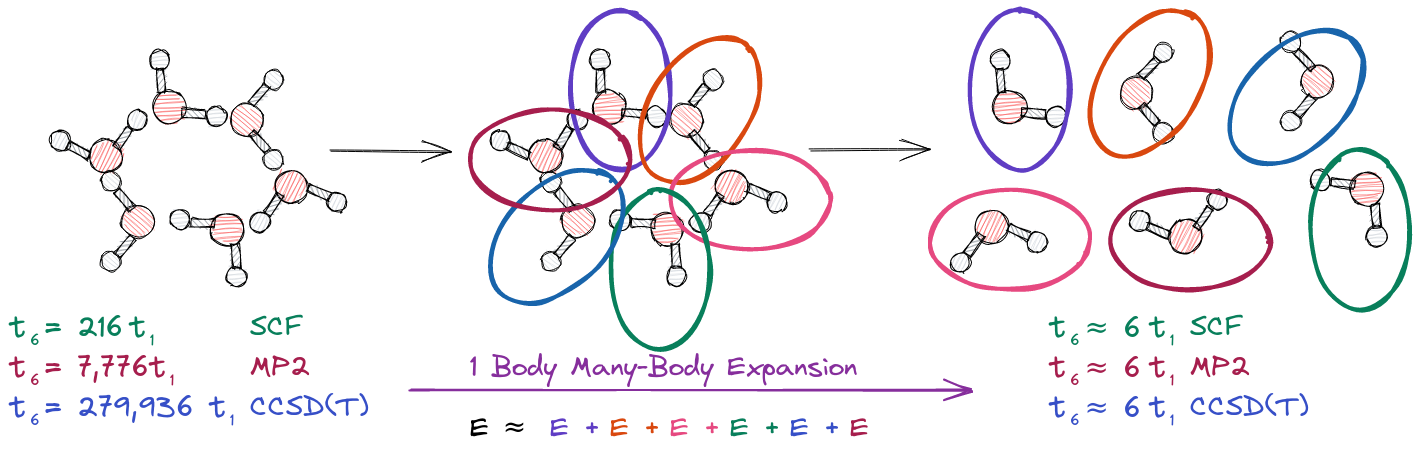
Fig. 1 Left. If \(t_1\) is the time it takes to compute the energy of a single water molecule, then \(t_6\) is the time required to compute the energy of water hexamer. Middle. In a 1-body many-body expansion (MBE), we approximate the energy of water hexamer as the sum of the energies of each water molecule. Right. The 1-body MBE approximation is dramatically cheaper to compute than the energy of the water hexamer.
The goal of quantum chemistry is to be able to predict and explain computational phenomenona using rigorous physical models that contain little to no emperical parameters. Unfortunately quantum chemistry methods exhibit steep computational scaling with respect to system size, \(N\). For example most modern self-consistent field (SCF) methods (e.g., Hartree-Fock or density functional theory) exhibit \(\mathcal{O}\left(N^3\right)\) scaling, which is to say that the time to solution for SCF methods increases cubically with respect to \(N\).
To better understand computational complexity, assume that for a particular quantum chemistry method \(t_1\) is the time to solution for computing the energy of a single water molecule. The left side of Fig. 1 shows how the time to solution for computing the energy of water hexamer, \(t_6\), compares to \(t_1\), for three quantum chemistry methods. For the purposes of Fig. 1 we assume that SCF scales as \(\mathcal{O}\left(N^3\right)\), second-order Moller-Plesset perturbation theory (MP2) scales as \(\mathcal{O}\left(N^5\right)\), and coupled cluster with single, double, and perturbative triple excitations, CCSD(T), scales as \(\mathcal{O}\left(N^7\right)\). For SCF, this means that \(t_6 = 6^3 t_1 =216 t_1\). That is to say, an SCF calculation on water hexamer will take 216 times longer than an SCF calculation on a single water molecule. The situation is markedly worse for CCSD(T) where we expect computing the energy of water hexamer to be 279,936 times longer than computing the energy of a single water molecule.
A solution?
While the exact electronic Hamiltonian is a pair-wise operator, for a given basis set the exact electron wavefunction has contributions arising from all possible excitations out of a reference state. In practice, excitations tend to contribute more to the wavefunction if the orbitals involved in the excitation are spatially local to one another. Thus, to reduce the scaling of an electronic structure method, one may somehow restrict the set of excitations considered to spatially local sets.
Conceptually one of the easiest ways to establish local sets is to fragment a molecule. In the full water hexamer calculation shown on the left side Fig. 1 each electron can see each orbital. The middle panel of Fig. 1 suggests that we instead treat water hexamer as six separate water molecules. By separate we mean the electrons in each water molecule can now only see the orbitals associated with that water molecule. In practice, this is somewhat trivial to implement, as it just amounts to running six individual calculations (one for each water molecule). As shown on the right side of Fig. 1, by fragmenting water hexamer, we can approximate the energy of the water hexamer at a cost of six times \(t_1\). Even for SCF this represents a reduction of two orders of magnitude in the time to solution; the savings are even more remarkable for high-accuracy CCSD(T) which sees a reduction in time of five orders of magnitude!
The approximation just described is known as a one-body method because the target system is broken up into fragments and those fragments are not allowed to interact with one another. As this description suggests the one-body approximation is usually not particularly accurate on account of neglecting the interactions among the various fragments. Unfortunately, for most use cases, a reduction in computational cost is only useful if the corresponding approximation is sufficiently accurate, and one-body fragment-based methods are rarely of interest.
The many-body expansion (MBE)
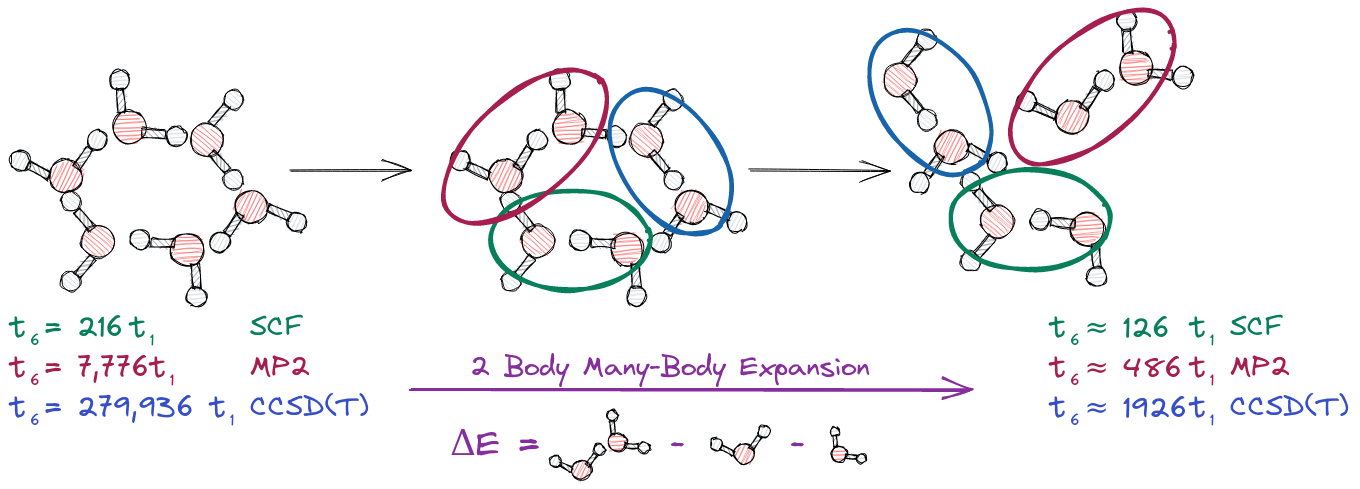
Fig. 2 Left. Time to solution \(t_6\) for water hexamer as a multiple of the time to solution for a single water molecule at the same level of theory \(t_1\). Middle. Three of the 15 possible dimers. Right. The time to solution for the two-body approximation.
As discussed at the end of the previous section, a one-body approximation is an insufficiently accurate approximation to energy of the target system on account of neglecting many-body interactions. Of the neglected interactions, the most important are the pair-wise interactions among the fragments, i.e., the two-body interactions.
Most fragment-based methods compute two-body interactions via a supersystem approach. Let \(IJ\) be the system formed from the union of fragments \(I\) and \(J\), then using a supersystem approach we can compute the two-body interaction between \(I\) and \(J\) by computing the energy of \(IJ\) and subtracting from it the sum of the energies of \(I\) and \(J\). Put another way, we remove the one-body contributions to the energy of \(IJ\) and what remains must be the two-body interaction. This is pictorially shown in the center of Fig. 2.
For water hexamer there is 6 choose 2, or 15, dimers (a dimer being a pair of fragments). Each pair of water molecules, or dimer, represents a system which is two times larger than a single fragment. Thus at the SCF level of theory, for example, the time to compute the energy of a dimer is \(2^3t_1=8t_1\). Since there are 6 fragments and 15 dimers involved in approximating the energy of the hexamer, the total time to approximate the energy of the water hexamer is now 126|t_1|.
While at the SCF level of theory the two-body approximation is two orders of magnitude more expensive than the one-body approximation, the resulting approximate energy is much better. Furthermore, the 15 dimer, and 6 monomer, calculations represent 21 separate calculations, which can easily be parallelized. Thus with access to sufficient parallel resources, at the SCF level of theory, the time for the two-body approximation can be reduced to \(8t_1\) with little trouble.
While the two-body approximation tends to be more accurate than the one-body approximation, for high-accuracy work the two-body approximation tends to still be insufficient. Using the supersystem method it is straightforward to compute three-body interactions by taking unions of three fragments, computing the energy, and then subtracting from that energy the two- and one-body contributions. The result is a three-body method. The superystem method can be extended to computing four-, five-, and six-body interactions. The resulting equation represents a formally exact energy expansion of the hexamer’s energy known as the many-body expansion (MBE). The MBE (and the closely related generalized MBE) is at the heart of all fragment-based methods.