Fragment Based Methods
Background
Traditional electronic structure theory methods (e.g., self-consistent field theory, Moller-Plesset perturbation theory, or coupled cluster theory) scale highly non-linearly with system size (i.e., number of atoms in the molecule you are simulating). As an example of non-linear scaling consider how the time to solution is affected by doubling the system size (e.g., computing the energy of two water molecules instead of one).
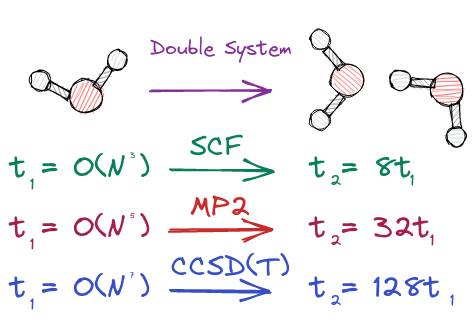
As illustrated if the time to compute the energy for one water molecule is \(t_1\), then the time to compute the energy for two water molecules, \(t_2\), is respectively 8, 32, and 128 times \(t_1\) for SCF, MP2, and CCSD(T)! The situation gets notably worse as you increase the system size. For example, the time to compute the energy of a water hexamer, \(t_6\) is respectively 216, 7,776, and 279,936 times \(t_1\) for for SCF, MP2, and CCSD(T).
Fragment based methods offer a seemingly simple means of skirting the highly non-linear scaling of traditional methods, i.e., instead of computing the energy of the total system all at once, we break the system up into “fragments”, compute the energy of each fragment, and approximate the energy of the system by the sum of the fragment energies. For water hexamer this is illustrated below.
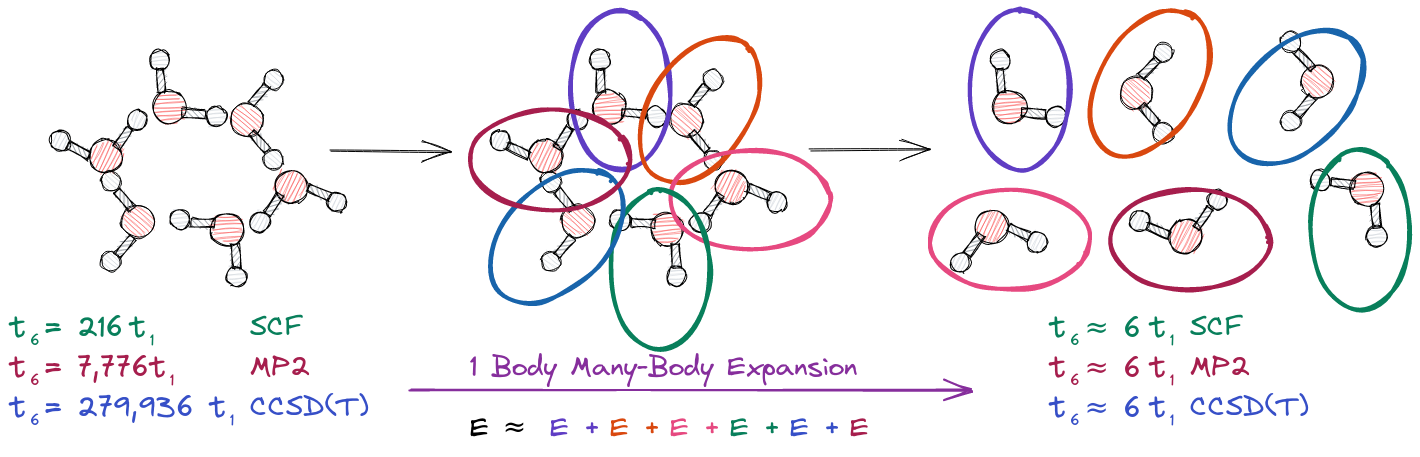
For water hexamer we break the system into six fragments (each water molecule is one fragment). The energy of each fragment is computed using a traditional electronic structure calculation. Thus by approximating the energy of the water hexamer by the sum of the energies of the water molecules, we our time to solution is simply six times \(t_1\). This approximation is known as a one-body many-body expansion (MBE). For SCF, MP2, and CCSD(T) using the one-body MBE to approximate the energy of the water hexamer respectively results in speed ups of 36, 1296, and 46656 over the traditional water hexamer calculation! The general form of the one-body MBE for \(N\) fragments is:
\[E \approx \sum_{I=1}^N E_{I}\]As you can probably imagine, a one-body MBE results in a relatively terrible approximate energy. We can improve on the one-body approximation by using a two-body approximation. This two-body approximation is illustrated below.
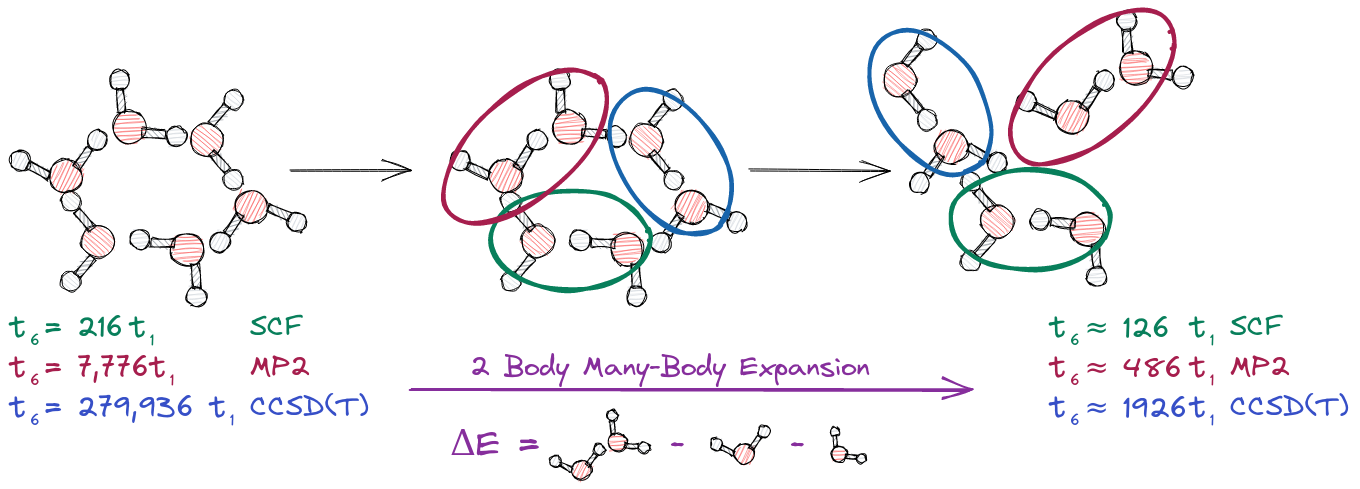
For the pair \(IJ\) formed from fragments \(I\) and \(J\) the two-body interaction of \(I\) with \(J\), \(\Delta E_{IJ}\), is given by:
\[\Delta E_{IJ} = E_{IJ} -E_{I} -E_{J}\]where \(E_{IJ}\) is the energy of the dimer, and \(E_I\) (\(E_J\)) is the energy of fragment \(I\) (\(J\)). In the two-body approximation we add to the one-body approximate energy all of the two-body interactions in the system. For our water hexamer example there are \({16 \choose 2} = 15\) two-body interactions. In addition to the calculations needed for the one-body MBE, each two-body interaction requires us to compute the energy of a dimer (as shown above each dimer requires 8, 32, and 128 time \(t_1\) at the SCF, MP2, and CCSD(T) levels of theory respectively). In turn, at the SCF, MP2, and CCSD(T) levels of theory we now have speedups of about 1.7, 16, and 145.3 over the traditional water hexamer calculation. It should be noted however that all of the fragment and dimer calculations involve independent invocations of an electronic structure package, and thus are easily parallelized. In turn, with sufficient computing resources, the apparent time to solution (i.e., how long you need to actually wait for the solution) can be reduced to 8, 32, or 128 \(t_1\) (i.e., the time for a single dimer calculation). Using such parallelization, the two-body MBE is 27, 243, and 2,187 times faster than the traditional water hexamer calculation. The general two-body MBE for \(N\) fragments is:
\[E \approx \sum_{I=1}^N E_{I} + \sum_{I<J} ^{N \choose 2} \Delta E_{IJ}\]In practice the two-body MBE is substantially more accurate than the one-body MBE, but it is usually still not sufficiently accurate for most chemical applications. As you may suspect, the two-body MBE can be improved upon by the three-body MBE. Conceptually the three-body MBE is similar to the two-body MBE. In the three-body MBE we additionally consider all three-body interactions. The three-body interaction among fragments \(I\), \(J\), and \(K\) is given by:
\[\Delta E_{IJK} = E_{IJK} - \Delta E_{IJ} - \Delta E_{IK} - \Delta E_{JK} - E_{I} - E_{J} - E_{K}\]which means that we must additionally compute the energy of each trimer of fragments. As is likely apparent at this point, we can then improve upon the three-body approximation with a four-body approximation, a five-body approximation, etc., up to an \(N\)-body approximation and the final energy expression is given by:
\[E = \sum_{I=1}^N E_{I} + \sum_{I<J} ^{N \choose 2} \Delta E_{IJ} + \sum_{I<J<K} ^{N \choose 4} \Delta E_{IJK} + \cdots\]where the ellipses encompass all of the many-body approximations involving more than three fragments. It should be noted that this is an exact equation, and thus we are guaranteed to recover the total energy. In practice, the full order MBE is rarely used outside of academic discussions and truncating the MBE at three-body (or rarely four-body) interactions usually suffices for most chemical applications.
Research Questions
The MBE affords a very promising avenue for circumventing, the highly non-linear scaling of traditional electronic structure methods; however, there are still a lot of research questions preventing wide-spread, black-box adoption of the MBE. Our group is currently trying to answer questions such as:
- How to best fragment an arbitrary system?
- How to reduce the number of dimer and trimer calculations required?
- How to avoid artifacts from the incompleteness of the basis set?
